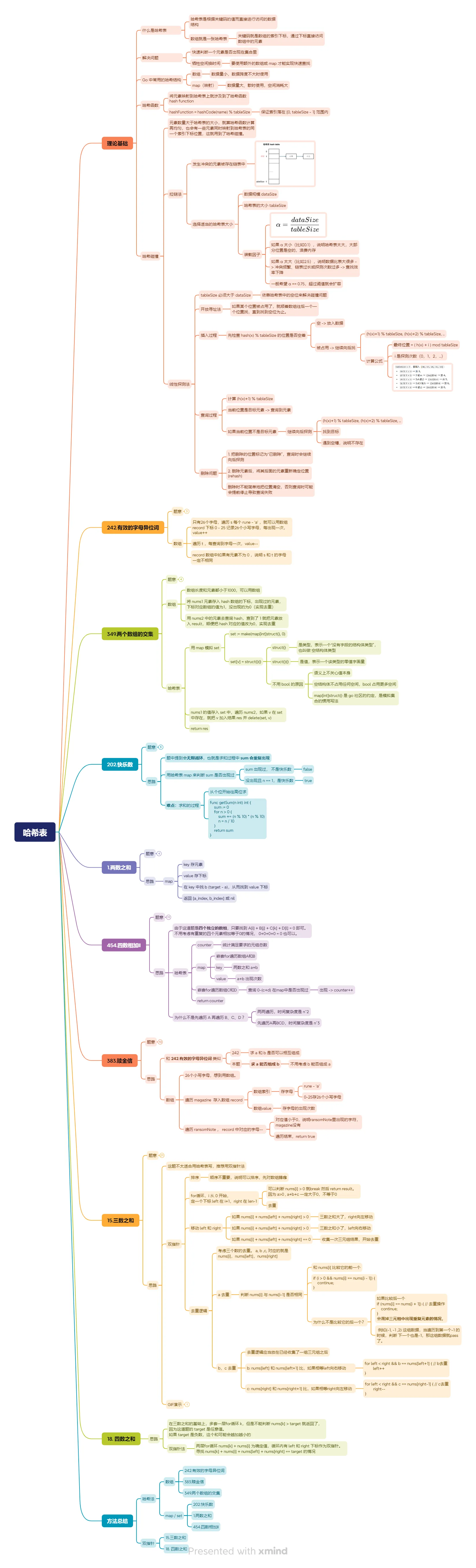
Table of Contents
三数之和和四数之和被放在哈希表章节中,但是其实不适合用哈希表来做,剪枝操作很麻烦。这里主要用双指针法来做。双指针法的好处是可以省一次 for 循环。 代码随想录 | 三数之和、四数之和
15. 三数之和
中等
给你一个整数数组
nums,判断是否存在三元组[nums[i], nums[j], nums[k]]满足i != j、i != k且j != k,同时还满足nums[i] + nums[j] + nums[k] == 0。请你返回所有和为0且不重复的三元组。**注意:**答案中不可以包含重复的三元组。
示例 1:
示例 2:
示例 3:
提示:
3 <= nums.length <= 3000-105 <= nums[i] <= 105
双指针法
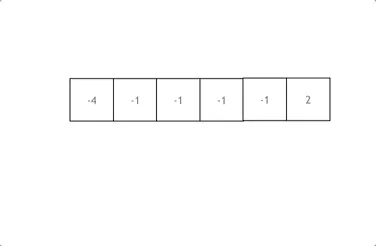
首先将数组排序,然后有一层for循环,i 从下标0的地方开始,left 在 i+1 的位置上, right 在 len-1 的位置上。
在数组中找到abc使得 a+b+c==0,这里 a = nums[i], b = nums[left], c = nums[right]。
首先判断 nums[i] 是否大于 0, 如果 a 大于0,那么 a+b+c 一定大于0。那么如何移动 left 和 right 呢?
这里需要注意 target > 0 才可以这样写。如果 target < 0,a < 0 也是可以找到三元组的。 例如 [-4, -1, 0], target == 5
如果 a+b+c > 0 说明三数之和大了,因为数组排序过,所以 right 应该向左移动,这样三数之和才能小一点。
如果 a+b+c < 0 说明三数之和小了,应该让 left 向右移动,这样三数之和才能大一点。
当 a+b+c == 0 时开始收集结果,在收集到一个结果之后去重,right 也是一样。
for left < right && nums[left] == nums[left+1] { left++}在 nums[left] 和 下一个数不同时,至少保证一次指针移动
完整代码
func threeSum(nums []int) [][]int { sort.Ints(nums) len := len(nums) result := [][]int{} for i := 0; i < len - 2; i++ { if nums[0] > 0 { break } // 如果 nums[i] 和前一个重复,则进行下一次循环 if i > 0 && nums[i] == nums[i - 1] { continue } left := i + 1 right := len - 1 for left < right { // 没有=,因为 left == right 时是一个数,不是三数之和了 if nums[i] + nums[left] + nums[right] == 0 { result = append(result, []int{nums[i], nums[left], nums[right]}) // 在收集到一个结果后去重 for left < right && nums[left] == nums[left+1] { left++ } for left < right && nums[right] == nums[right-1] { right-- } // 在 nums[left] 和 下一个数不同时,至少保证一次指针移动 left++ right-- } else if nums[i] + nums[left] + nums[right] > 0 { right-- } else { left++ } } } return result}哈希解法(未完成)
func threeSum(nums []int) [][]int { res := make([][]int, 0) sort.Ints(nums) // 找出a + b + c = 0 // a = nums[i], b = nums[j], c = -(a + b) for i := 0; i < len(nums); i++ { // 排序之后如果第一个元素已经大于零,那么不可能凑成三元组 if nums[i] > 0 { break } // 三元组元素a去重 if i > 0 && nums[i] == nums[i-1] { continue } set := make(map[int]struct{}) for j := i + 1; j < len(nums); j++ { // 三元组元素b去重 if j > i + 2 && nums[j] == nums[j-1] && nums[j-1] == nums[j-2] { continue } c := -nums[i] - nums[j] if _, ok := set[c]; ok { res = append(res, []int{nums[i], nums[j], c}) // 三元组元素c去重 delete(set, c) } else { set[nums[j]] = struct{}{} } } } return res}18.四数之和
中等
给你一个由
n个整数组成的数组nums,和一个目标值target。请你找出并返回满足下述全部条件且不重复的四元组[nums[a], nums[b], nums[c], nums[d]](若两个四元组元素一一对应,则认为两个四元组重复):
0 <= a, b, c, d < na、b、c和d互不相同nums[a] + nums[b] + nums[c] + nums[d] == target你可以按 任意顺序 返回答案 。
示例 1:
示例 2:
提示:
1 <= nums.length <= 200-109 <= nums[i] <= 109-109 <= target <= 109
双指针法
这道题同样使用双指针的思路,就是在 三数之和 的基础上再套一层 for 循环。但是需要注意,四数之和 的 target 不是 0 是可以变的,这时就不能直接根据 n1 > target 来确定没有符合要求的四元组了。因为 target 可能为负数,所以四数之和也可能是越加越小的。
如果 target < 0,a < 0 也是可以找到三元组的。 例如 [-4, -1, 0], target == 5
可以把 a + b 当成一个整体来剪枝,但是剪枝是非必要操作。
if (nums[k] + nums[i] > target && nums[k] + nums[i] >= 0) { break;}另外在去重的时候,边界也有所更改。例如对 b 去重时,(i := k + 1)需要 i > k+1,因为要取 nums[i - 1], i 必须大于 k 。
完整代码
func fourSum(nums []int, target int) [][]int { len := len(nums) res := [][]int{} if len < 4 { return nil } sort.Ints(nums) for k := 0; k < len - 3; k++ { n1 := nums[k] // if n1 > target { // 不能这样写,因为 target 可能是负数 // break // } if k > 0 && n1 == nums[k-1] { // 对 nums[k] 去重 continue } for i := k + 1; i < len - 2; i++ { n2 := nums[i] if i > k + 1 && n2 == nums[i-1] { // 对 nums[i] 去重 continue } left := i + 1 right := len - 1 for left < right { n3 := nums[left] n4 := nums[right] sum := n1 + n2 + n3 + n4 if sum < target { left++ } else if sum > target { right-- } else { res = append(res, []int{n1, n2, n3, n4}) for left < right && n3 == nums[left+1] { // left 去重 left++ } for left < right && n4 == nums[right-1] { // right 去重 right-- } // 找到答案时,双指针同时靠近 left++ right-- } } } } return res}哈希表章节总结