459. 重复的子字符串

459. 重复的子字符串

简单

给定一个非空的字符串 s ，检查是否可以通过由它的一个子串重复多次构成。

示例 1:

输入: s = "abab"
输出: true
解释: 可由子串 "ab" 重复两次构成。

示例 2:

输入: s = "aba"
输出: false

示例 3:

输入: s = "abcabcabcabc"
输出: true
解释: 可由子串 "abc" 重复四次构成。 (或子串 "abcabc" 重复两次构成。)

提示：

• 1 <= s.length <= 104
• s 由小写英文字母组成

暴力解法

s 如果是周期串，要找的 substr 一定满足以下要求：

• substr 包括 s 的第一个字符和最后一个字符，所以只需遍历 substr 的结尾字符，不用遍历开头。
• substr 的长度不得超过 len(s) 的一半，否则s不可能是周期串。
• substr 的长度必须被 len(s) 整除

虽然是暴力解法，但也做了相应的剪枝操作，时间复杂度是 O(n^2)。

is_match := true 这个初始值虽然方便，但是总感觉初始值设为 true 不太好。

func repeatedSubstringPattern(s string) bool {
    // 寻找子串，包含开头，结尾不超过中间，否则不可能由子串重复构成
    n := len(s)
    for l := 1; l <= n/2; l++ {
        if n % l != 0 { // 必须整除，否则不可能由该子串重复构成
            continue
        }
        substr := s[:l]
        is_match := true
        // 检查每一段是不是和 substr 相等
        for i := l; i < n; i = i + l {
            if s[i:i+l] != substr {
                is_match = false
                break
            }
        }
        if is_match {
            return true
        }
    }
    return false
}

双倍字符串法

把字符串翻倍，掐头去尾，如果原字符串在其中，那么原字符串就是周期串 。

这里直接使用库函数来查找字符串，实际上就是力扣 28 题。

具体代码：

func repeatedSubstringPattern(s string) bool {
    // 如果2个s拼起来掐头去尾，可以在其中找到s，就说明s是周期串
    t := s + s
    return strings.Contains(t[1:len(t)-1], s)
}

具体解释可以看 🔗周期字符串问题（两种方法），以下内容为搬运。

双倍字符串方法 ¶

把字符串翻倍，掐头去尾，如果原字符串在其中，那么原字符串就是周期串 。

假设字符串是 s ，把它的头尾字符分别染上黄色和蓝色：

把字符串 s 接到自身后面，然后掐头去尾，形成新字符串 s'：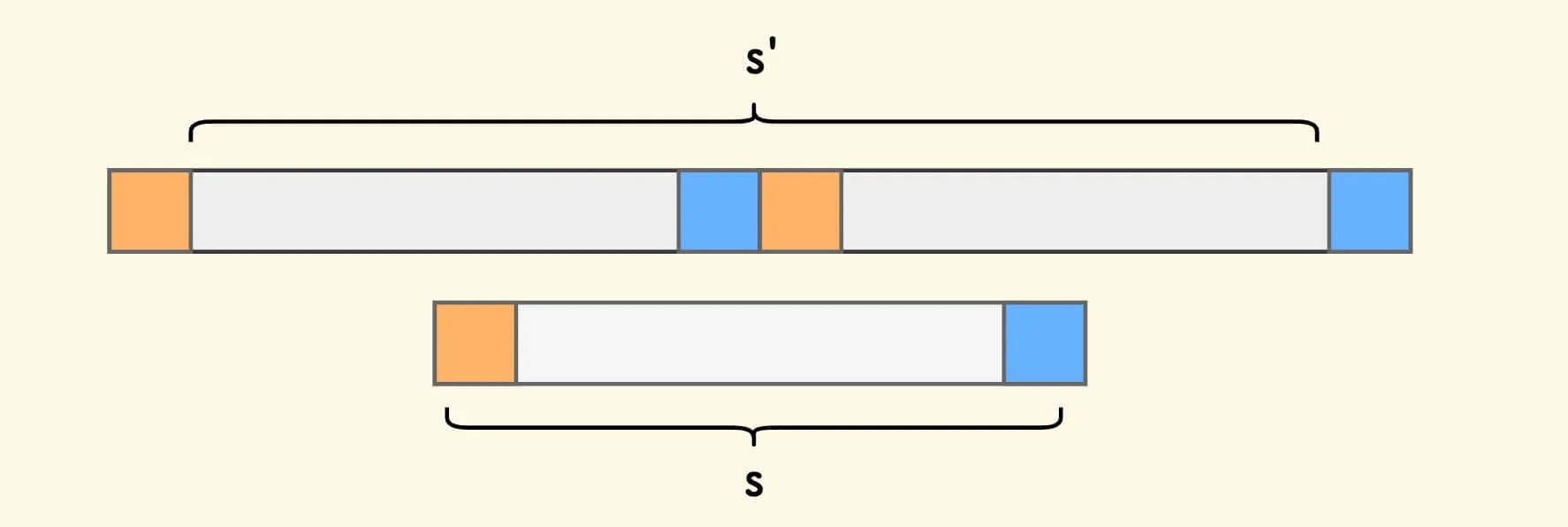

匹配意味着周期性

下面讨论原字符串 s 在新字符串 s' 中存在的情况。

一步一步对各部分涂色，使得相等的字符串颜色一样 。

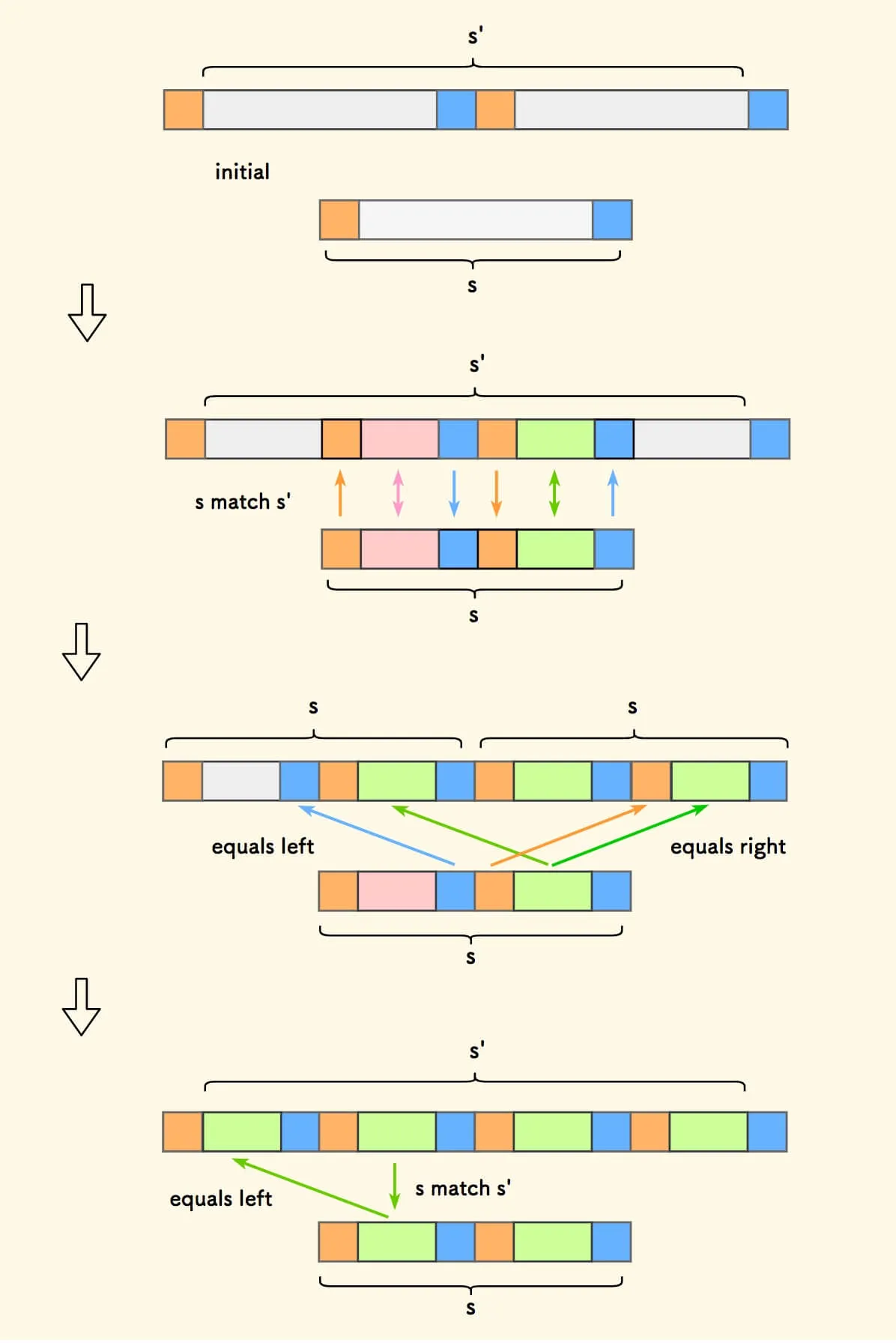
经过几轮的染色，可以看到最终 s 确实是一个周期串。

是否巧合？可以做一般性说明。

下图，不妨设右边匹配的少一些。对其中的任一字符 A ，可以按照如下的规则推演：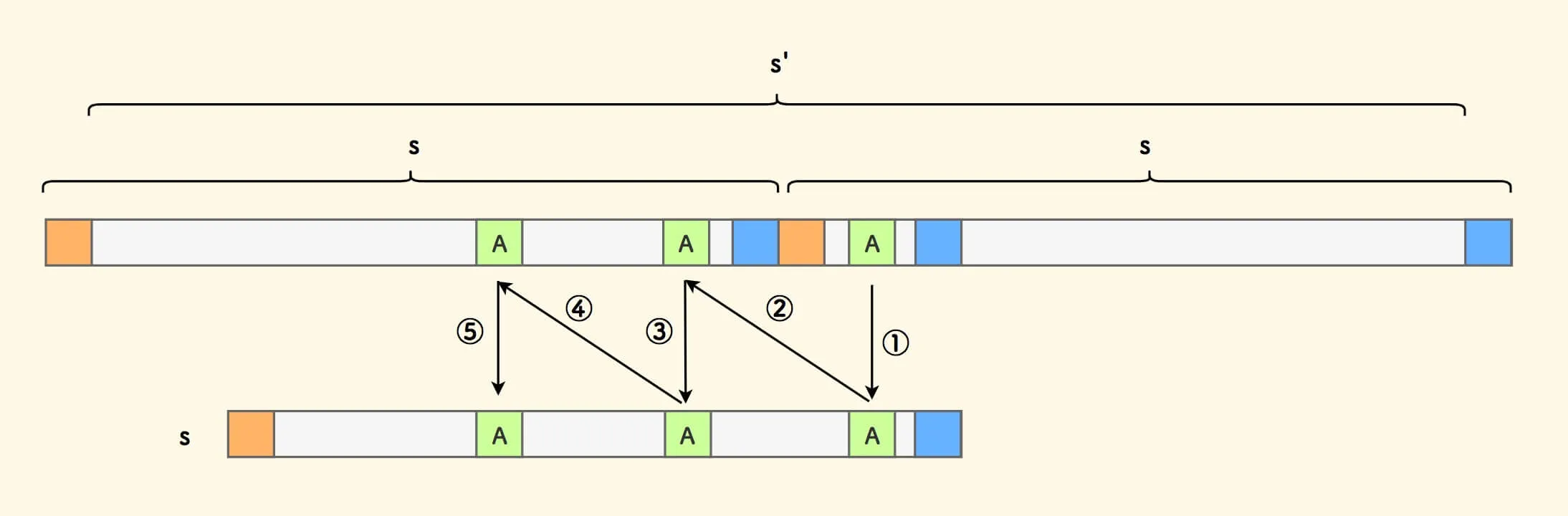

推演的细致说明：

• ① 号推演，由于上下字符串匹配。

• ② 号推演，由于和左上方的自身相等。

• 如此反复推演。

如此，任一此区间上的字符 A 会在 s 中周期性出现。

即说明字符串 s 是周期串。

周期性意味着匹配

反过来，如果一个字符串 s 是周期串，那么它一定在对应的 s' 中吗？

任何一个周期串可以表达为： 由某个模式子串的重复多次构成 。

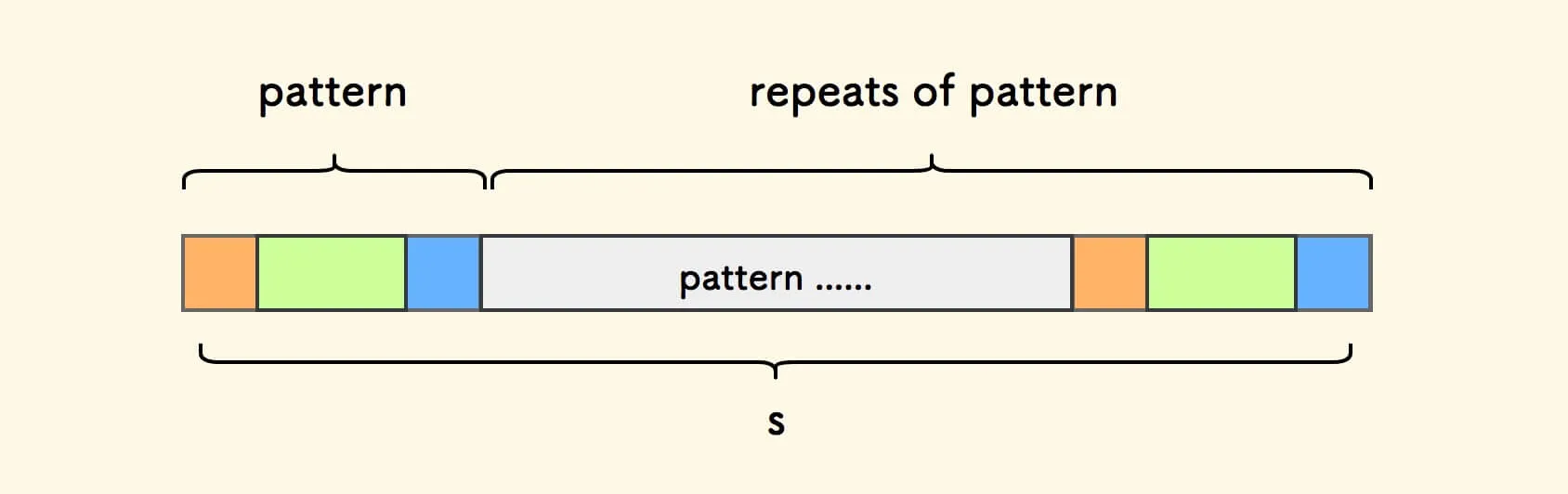
将周期串 s 的头字符对齐在第一个模式串后面， 每次右移一个模式串的长度。

可知，s 会在 s' 中有匹配，且可以有多个匹配。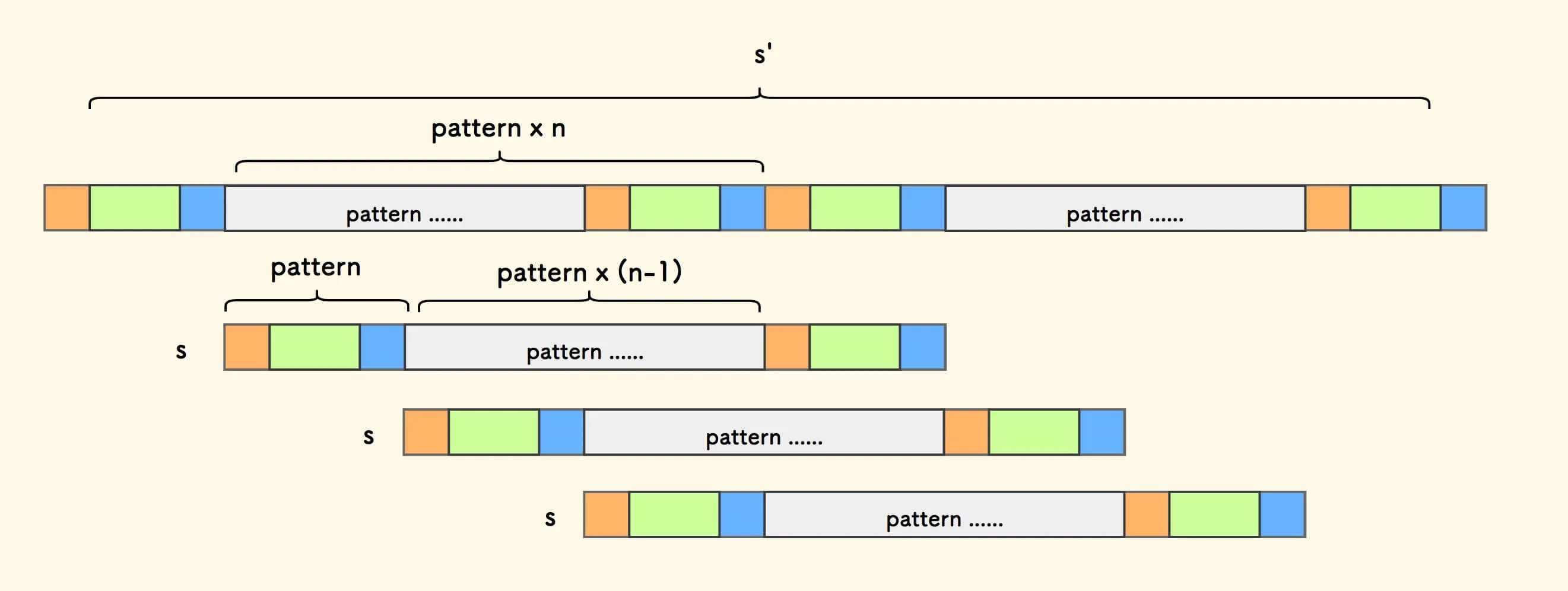

图中可看出， 因为模式串重复 n 次，所以会有 n 次匹配 。

构造双倍串 s' 时，移除头尾字符， 正是为了剔除最左和最右的两次必然匹配。 只有中间的 n 次匹配才用到了周期串重复模式串的性质。

结论

综上两方面说明了充分性和必要性，结论：

如果字符串在其掐头去尾的双倍字符串中，它就是周期串 。

KMP算法

如果一个字符串 s 是由重复子串组成，那么最长相等前后缀不包含的子串一定是字符串 s 的最小重复子串。

具体原因看 🔗代码随想录_重复的子字符串 和 🔗bilibili_字符串这么玩，可有点难度！ | LeetCode：459.重复的子字符串

具体代码：

func repeatedSubstringPattern(s string) bool {
    // 求 next 数组
    n := len(s)
    next := make([]int, n)
    j := 0
    next[0] = j
    for i := 1; i < n; i++ {
        for j > 0 && s[j] != s[i] {
            j = next[j-1]
        }
        if s[j] == s[i] {
            j++
        }
        next[i] = j
    }
    // next[n-1] 是s最长相等前后缀的长度
    if next[n-1] != 0 && n % (n - next[n-1]) == 0 {
        return true
    }
    return false
}

Xmind 总结

🔗Xmind 源文件