二叉树的前/中/后序遍历（深度优先遍历）

力扣题目链接

🔗144.二叉树的前序遍历(opens new window)

🔗145.二叉树的后序遍历(opens new window)

🔗94.二叉树的中序遍历

[TOC]

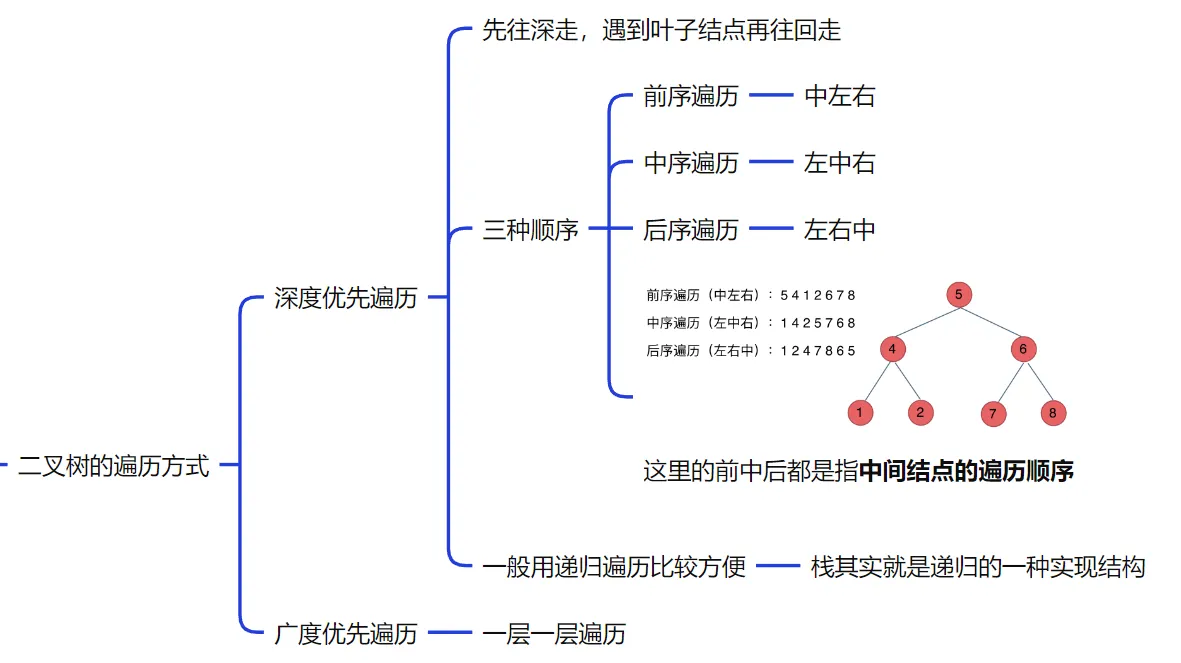
递归遍历

写递归遍历一定要确定以下3点：

确定递归函数的参数和返回值：确定哪些参数是递归的工程中需要处理的，就在递归函数中加上这个参数；明确每次递归的返回值，从而确定递归函数的返回类型。
确定终止条件：运行递归时遇到栈溢出错误，一般就是没写终止条件或终止条件写的不对。操作系统是用一个栈结构来保存每一层的递归信息，如果递归没有终止，操作系统的内存栈必然会溢出。
确定单层递归的逻辑：确定每一层递归需要处理的信息，在这里也就会重复调用自己来实现递归的过程。

前序遍历

在 Go 中如果使用命名返回值（给返回值起了名字 res，并且类型是 []int），相当于在函数内部自动声明了一个变量 res ，类型为 []int ，自动分配内存，并初始化为对应类型的零值 nil。

函数变量声明 var traversal func(node *TreeNode)

声明一个变量 traversal ，它的类型是 func(node *TreeNode)，也就是“接受一个*TreeNode参数，没有返回值”的函数类型。
后续再给它赋值一个具体的函数实现。

通常在匿名函数递归中使用，因为 Go 中的匿名函数不能在函数内调用自己，因此要先声明一个函数变量，再赋值匿名函数。

这样不用在外部声明递归函数，也不需要传指针了。

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func preorderTraversal(root *TreeNode) (res []int) {
    var traversal func(node *TreeNode)
    traversal = func(node *TreeNode) {
        // 确定终止条件
        if node == nil {
            return
        }
        // 确定单层递归的逻辑
        res = append(res, node.Val)// 中
        // 左
        traversal(node.Left)
        // 右
        traversal(node.Right)
    }
    traversal(root)
    return res
}

后序遍历

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func postorderTraversal(root *TreeNode) (res []int) {
    var traversal func(node *TreeNode)
    traversal = func(node *TreeNode) {
        // 确定终止条件
        if node == nil {
            return
        }
        // 确定单层递归的逻辑
        // 左
        traversal(node.Left)
        // 右
        traversal(node.Right)
        res = append(res, node.Val)// 中
    }
    traversal(root)
    return res
}

中序遍历（尝试外部递归函数）

三道题目一样都可以用匿名递归函数解决，这里尝试使用外部定义的递归函数来实现。

func inorderTraversal(root *TreeNode) []int {
    res := []int{}
    traversal(root, &res)
    return res
}

func traversal(cur *TreeNode, res *[]int) {
    // 确定终止条件
    if cur == nil {
        return
    }
    // 确定每层递归逻辑
    traversal(cur.Left, res) // 左
    *res = append(*res, cur.Val) // 中
    traversal(cur.Right, res) // 右
}

迭代遍历

在计算机中递归就是用栈实现的：递归的实现就是：每一次递归调用都会把函数的局部变量、参数值和返回地址等压入调用栈中，然后递归返回的时候，从栈顶弹出上一次递归的各项参数，所以这就是递归为什么可以返回上一层位置的原因。

因此用栈就可以实现二叉树的前后中序遍历了。

前序遍历—迭代法

前序遍历是「中左右」，每次先处理根节点，在处理左、右。那么就可以先把根节点放入栈中，再把右孩子加入栈，再加入左孩子。因为栈是先入后出，先加入右孩子才能保证出栈的时候是「中左右」的顺序

注意空节点不入栈，因为要对左右孩子操作，如果空节点入栈就操作空指针了。

用到了 List 包来作为栈。

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func preorderTraversal(root *TreeNode) []int {
    res := []int{}
    if root == nil {
        return res
    }
    st := list.New()
    st.PushBack(root)
    for st.Len() > 0 {
        // func (l *List) Remove(e *Element) any
        // 如果e是列表l的一个元素，Remove方法将e从l中移除，并返回元素值e.Value。该元素不能是nil。
        // any 需要断言成需要的类型
        node := st.Remove(st.Back()).(*TreeNode) // pop 栈顶元素
        res = append(res, node.Val)

        // 把右、左孩子放入栈
        if node.Right != nil {
            st.PushBack(node.Right)
        }
        if node.Left != nil {
            st.PushBack(node.Left)
        }
    }
    return res
}

后序遍历—迭代法

前序遍历最后数组的顺序是「中左右」，那么把左右调换位置「中右左」，再把res数组 reverse 一下就变成了后序遍历「左右中」的输出顺序。

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func postorderTraversal(root *TreeNode) []int {
    res := []int{}
    if root == nil {
        return res
    }
    st := list.New()
    st.PushBack(root)
    for st.Len() > 0 {
        // func (l *List) Remove(e *Element) any
        // 如果e是列表l的一个元素，Remove方法将e从l中移除，并返回元素值e.Value。该元素不能是nil。any 需要断言成需要的类型
        node := st.Remove(st.Back()).(*TreeNode) // pop 栈顶元素
        res = append(res, node.Val)

        // 前序遍历最后数组的顺序是 中左右，那么把左右调换位置「中右左」，再把res数组 reverse 一下就变成了后序遍历「左右中」
        if node.Left != nil {
            st.PushBack(node.Left)
        }
        if node.Right != nil {
            st.PushBack(node.Right)
        }

    }
    return reverse(res)
}

func reverse(s []int) []int {
    left := 0
    right := len(s) - 1
    for left < right {
        s[left], s[right] = s[right], s[left]
        left++
        right--
    }
    return s
}

中序遍历—迭代法

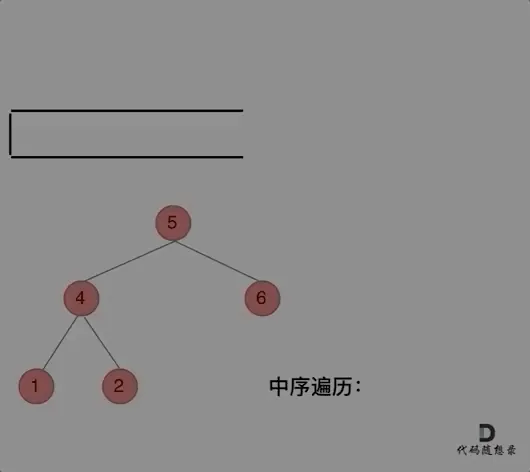
和迭代法前、后序遍历不同，迭代法中序遍历需要遍历过程和处理过程分开。

声明一个 cur TreeNode ，把它当指针遍历二叉树的左孩子，一边遍历一边把它放进栈中，一路向左~~（一路向西）~~走到黑，直到 cur.Left == nil。

此时 cur 就是「中」，弹出 cur 写入 result 数组（处理元素），cur = cur.Right，再继续遍历 cur 的左孩子……

（当 cur.Left == nil 时，左节点已经在上一步处理过了，此时 cur 就是中节点，需要处理的就是中节点。cur.Right 相当于一个「新的二叉树」，需要从它的左孩子遍历）

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func inorderTraversal(root *TreeNode) []int {
    res := []int{}
    if root == nil {
        return res
    }
    st := list.New()
    cur := root

    for cur != nil || st.Len() > 0 {
        if cur != nil {
            st.PushBack(cur)
            cur = cur.Left
        } else {
            cur = st.Remove(st.Back()).(*TreeNode)
            res = append(res, cur.Val)
            cur = cur.Right
        }
    }
    return res
}

# 二叉树的前/中/后序遍历（深度优先遍历）