二叉树的层序遍历（广度优先遍历）

二叉树的层序遍历——使用队列

层序遍历一个二叉树，就是从左到右一层一层地遍历二叉树，需要用队列来实现。

可以用 slice 或 list 来模拟队列。

队列先进先出，符合一层一层遍历的逻辑，广度优先逻辑。

栈先进后出，适合模拟深度优先遍历，也就是递归的逻辑。

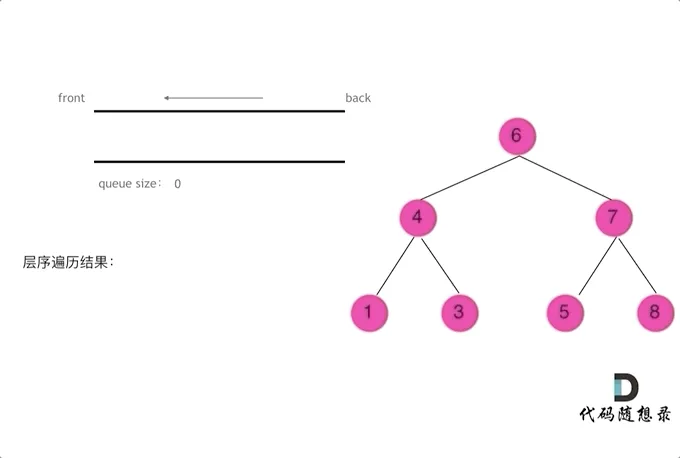
102.二叉树的层序遍历

🔗102.二叉树的层序遍历_LeetCode

给你二叉树的根节点 root ，返回其节点值的 层序遍历 。（即逐层地，从左到右访问所有节点）。

用切片模拟队列

先判断 root 如果为空则返回 nil；root 不为空则把 root 放入 queue 中。

第一层 for 循环在队列中没有元素时终止

第二层 for 循环需要提前确定 size 的数值，而不能直接用 len(queue)，因为 queue 中的元素是实时在变化的。其实这里用 for range size 更合适，之后的题目大多用了这个。

处理队列中的元素:

确定好该层的元素个数，循环弹出队列中第一个元素，记录它的值（并做相关操作），如果 node 有 Left 和 Right 则放入队列中。

最后把每层收集到的数组放入 result 中返回。

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func levelOrder(root *TreeNode) [][]int {
    result := [][]int{}
    if root == nil {
        return result
    }
    queue := []*TreeNode{}
    queue = append(queue, root)

    for len(queue) > 0 {
        size := len(queue)
        curLevelVal := []int{}
        for size > 0 {
            // 弹出队列第一个元素
            a := queue[0]
            curLevelVal = append(curLevelVal, a.Val)
            queue = queue[1:]
            if a.Left != nil {
                queue = append(queue, a.Left)
            }
            if a.Right != nil {
                queue = append(queue, a.Right)
            }
            size--
        }
        result = append(result, curLevelVal)
    }
    return result
}

107.二叉树的层次遍历II

🔗107.二叉树的层次遍历II_LeetCode

给你二叉树的根节点 root ，返回其节点值 自底向上的层序遍历 。（即按从叶子节点所在层到根节点所在的层，逐层从左向右遍历）

就是上面的 102 题的结果反转一下。

这次用 container 中的 list 来模拟队列。

func levelOrderBottom(root *TreeNode) [][]int {
    result := [][]int{}

    if root == nil {
        return nil
    }
    queue := list.New() //这里的list是包名，不是List类型
    queue.PushBack(root)

    for queue.Len() > 0 {
        curLevelVal := []int{} // 用于存储当前层节点值
        size := queue.Len() // 保存当前层的节点个数，再循环操作该层节点
        for range size { // 这个循环结束也就代表处理完该层元素了
            // Element结构体是链表List中的一个元素，里面的 Val 才是存的值，所以在 Remove() 时传入的是元素指针，不会出现相等元素删除错误的情况
            // 弹出队列第一个元素
            node := queue.Remove(queue.Front()).(*TreeNode)
            curLevelVal = append(curLevelVal, node.Val)
            if node.Left != nil {
                queue.PushBack(node.Left)
            }
            if node.Right != nil {
                queue.PushBack(node.Right)
            }
        }
        // 这层处理完了，把这层的节点值数组放进 result 中
        result = append(result, curLevelVal)
    }

    return reverse(result)
}

func reverse(s [][]int) [][]int {
    left := 0
    right := len(s)-1
    for left < right {
        s[left], s[right] = s[right], s[left]
        left++
        right--
    }
    return s
}

199.二叉树的右视图

🔗199.二叉树的右视图_LeetCode

给定一个二叉树的 根节点 root，想象自己站在它的右侧，按照从顶部到底部的顺序，返回从右侧所能看到的节点值。

相同的遍历思路，只记录队列中的该层元素的最后一个（最右侧的）节点值。

func rightSideView(root *TreeNode) []int {
    result := []int{}
    if root == nil {
        return nil
    }
    queue := list.New()
    queue.PushBack(root)

    for queue.Len() > 0 {
        size := queue.Len()
        for i := range size { // 遍历该层元素
            node := queue.Remove(queue.Front()).(*TreeNode)
            if node.Left != nil {
                queue.PushBack(node.Left)
            }
            if node.Right != nil {
                queue.PushBack(node.Right)
            }
            // 只记录队列中的该层元素的最后一个（最右侧的）节点值
            if i == size - 1 {
                result = append(result, node.Val)
            }
        }
    }
    return result
}

637.二叉树的层平均值

🔗637.二叉树的层平均值_LeetCode

给定一个非空二叉树的根节点 root , 以数组的形式返回每一层节点的平均值。与实际答案相差 10-5 以内的答案可以被接受。

同 102 思路，给每层的结果分别计算一下平均值。

func averageOfLevels(root *TreeNode) []float64 {
    result := []float64{}
    if root == nil {
        return nil
    }

    queue := list.New()
    queue.PushBack(root)

    for queue.Len() > 0 {
        size := queue.Len()
        curLevelVals := []int{}
        for range size {
            node := queue.Remove(queue.Front()).(*TreeNode)
            curLevelVals = append(curLevelVals, node.Val)
            if node.Left != nil {
                queue.PushBack(node.Left)
            }
            if node.Right != nil {
                queue.PushBack(node.Right)
            }
        }
        // 计算该层数值平均值
        sum := 0
        for i := range len(curLevelVals) {
            sum += curLevelVals[i]
        }
        var avg float64
        avg = float64(sum) / float64(len(curLevelVals))
        result = append(result, avg)
    }
    return result
}

429.N叉树的层序遍历

🔗429.N叉树的层序遍历_LeetCode

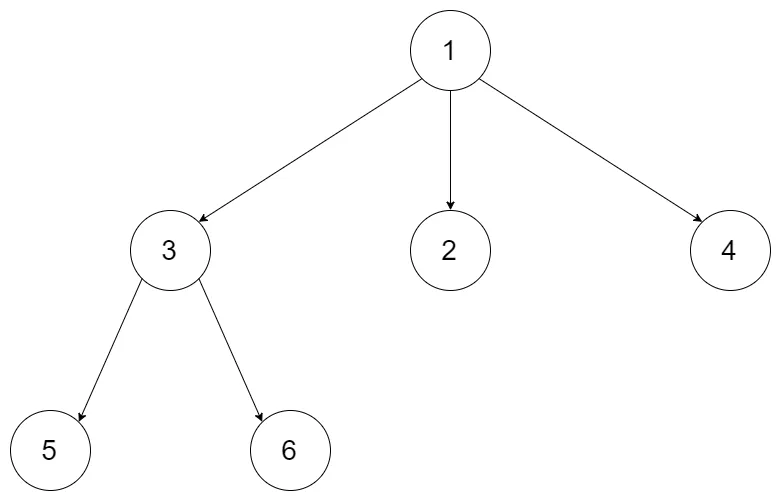
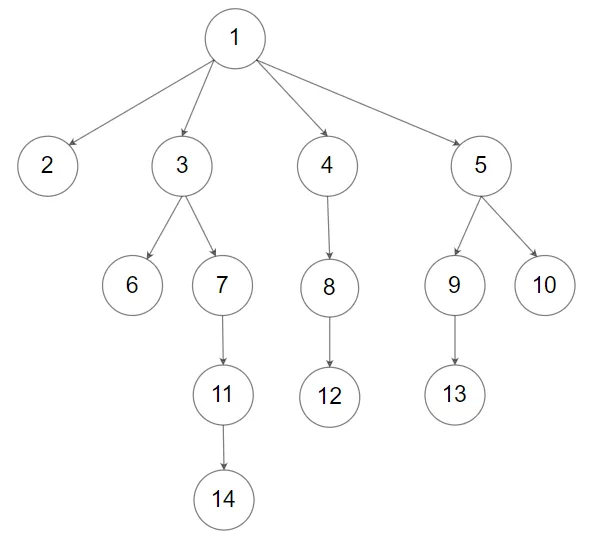
给定一个 N 叉树，返回其节点值的层序遍历。（即从左到右，逐层遍历）。

树的序列化输入是用层序遍历，每组子节点都由 null 值分隔（参见示例）。

示例 1：
输入：root = [1,null,3,2,4,null,5,6]
输出：[[1],[3,2,4],[5,6]]
示例 2：
输入：root = [1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14]
输出：[[1],[2,3,4,5],[6,7,8,9,10],[11,12,13],[14]]

处理节点时，用遍历切片的方式代替之前的 Left、Right 判断。

func levelOrder(root *Node) [][]int {
    if root == nil {
        return nil
    }
    result := [][]int{}
    queue := list.New()
    queue.PushBack(root)

    for queue.Len() > 0 {
        size := queue.Len()
        curLevelVals := []int{}
        for range size {
            node := queue.Remove(queue.Front()).(*Node)
            curLevelVals = append(curLevelVals, node.Val)
            if node.Children != nil {
                for i := range node.Children {
                    queue.PushBack(node.Children[i])
                }
            }
        }
        result = append(result, curLevelVals)
    }
    return result
}

515.在每个树行中找最大值

🔗515.在每个树行中找最大值_LeetCode

给定一棵二叉树的根节点 root ，请找出该二叉树中每一层的最大值。

在遍历每一层的 node 时顺便做最大值的判断。

也可以在 102 的结果上做最大值判断，只不过会多一次 for 循环。

func largestValues(root *TreeNode) []int {
    if root == nil {
        return nil
    }
    result := []int{}
    queue := list.New()
    queue.PushBack(root)


    for queue.Len() > 0 {
        temp := math.MinInt64
        size := queue.Len()
        curLevelVals := []int{}
        for range size {
            node := queue.Remove(queue.Front()).(*TreeNode)
            curLevelVals = append(curLevelVals, node.Val)
            temp = max(temp, node.Val)

            if node.Left != nil {
                queue.PushBack(node.Left)
            }
            if node.Right != nil {
                queue.PushBack(node.Right)
            }
        }
        // 取最大值
        result = append(result, temp)
    }
    return result
}

func max(x, y int) int {
    if x > y {
        return x
    }
    return y
}

116.填充每个节点的下一个右侧节点指针

🔗116.填充每个节点的下一个右侧节点指针_LeetCode

给定一个 完美二叉树 ，其所有叶子节点都在同一层，每个父节点都有两个子节点。二叉树定义如下：
struct Node {
  int val;
  Node *left;
  Node *right;
  Node *next;
}
填充它的每个 next 指针，让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点，则将 next 指针设置为 NULL。

初始状态下，所有 next 指针都被设置为 NULL。

示例 1：
输入：root = [1,2,3,4,5,6,7]
输出：[1,#,2,3,#,4,5,6,7,#]
解释：给定二叉树如图 A 所示，你的函数应该填充它的每个 next 指针，以指向其下一个右侧节点，如图 B 所示。序列化的输出按层序遍历排列，同一层节点由 next 指针连接，'#' 标志着每一层的结束。
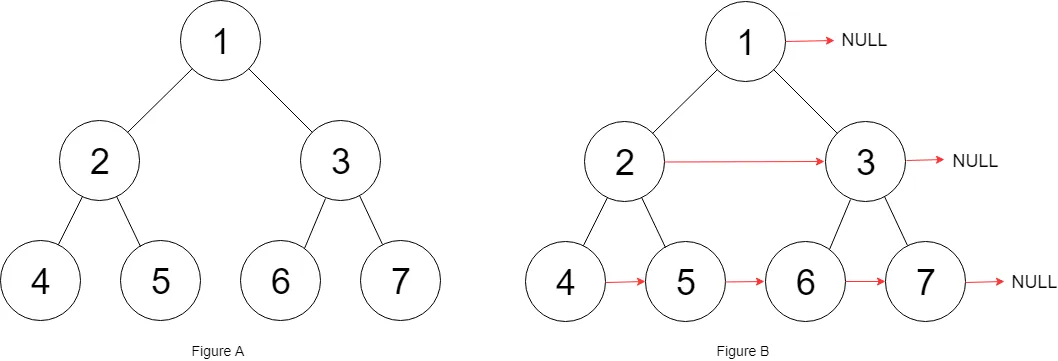
示例 2:
输入：root = []
输出：[]

处理每一层元素时：

if i < size - 1 即此时的 node.Next 还有节点，不为 nil，把 node.Next 指向后面那个节点。这时 node 已经被弹出队列了，因此它原先的下一个节点，就是 queue 现在的第一个节点，读取它并类型断言为 *Node。

node.Next = queue.Front().Value.(*Node)

否则（i >= size -1），此时的 node.Next 为 nil。 i == size -1 时，这个 node 是 queue 中仅有的一个元素，因此 node.Next == nil。

就这样把每一层的节点都指向它队列中的下一个节点，末尾节点指向 nil 即可

func connect(root *Node) *Node {
  if root == nil {
        return nil
    }
    queue := list.New()
    queue.PushBack(root)
    for queue.Len() > 0 {
        size := queue.Len()
        for i := range size {
            node := queue.Remove(queue.Front()).(*Node)
            if i < size - 1 {
                node.Next = queue.Front().Value.(*Node)
            } else {
                node.Next = nil
            }

            if node.Left != nil {
                queue.PushBack(node.Left)
            }
            if node.Right != nil {
                queue.PushBack(node.Right)
            }
        }
    }
    return root
}

117.填充每个节点的下一个右侧节点指针II

🔗117.填充每个节点的下一个右侧节点指针II_LeetCode

给定一个二叉树：
struct Node {
  int val;
  Node *left;
  Node *right;
  Node *next;
}
填充它的每个 next 指针，让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点，则将 next 指针设置为 NULL 。

初始状态下，所有 next 指针都被设置为 NULL 。

示例 1：
输入：root = [1,2,3,4,5,null,7]
输出：[1,#,2,3,#,4,5,7,#]
解释：给定二叉树如图 A 所示，你的函数应该填充它的每个 next 指针，以指向其下一个右侧节点，如图 B 所示。序列化输出按层序遍历顺序（由 next 指针连接），'#' 表示每层的末尾。
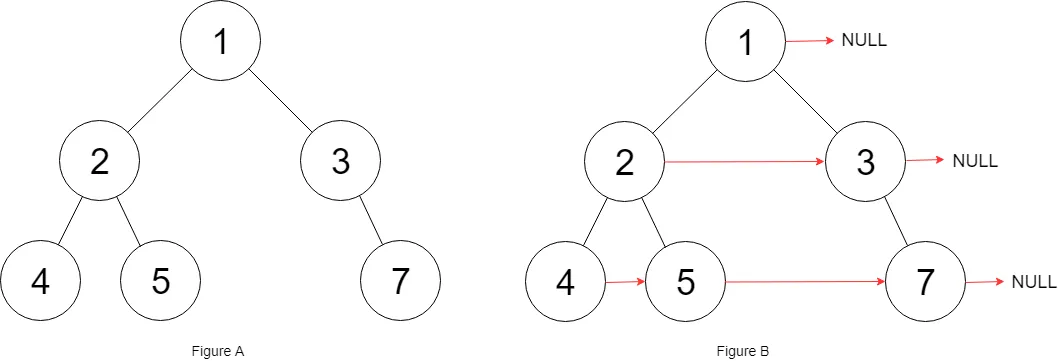
示例 2：
输入：root = []
输出：[]

同116。

104.二叉树的最大深度

🔗104.二叉树的最大深度_LeetCode

给定一个二叉树 root ，返回其最大深度。

二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。

示例 1：
输入：root = [3,9,20,null,null,15,7]
输出：3
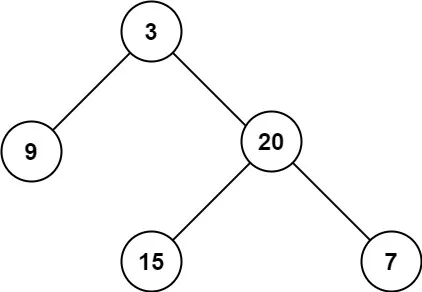
示例 2：
输入：root = [1,null,2]
输出：2
提示：

树中节点的数量在 [0, 104] 区间内。

-100 <= Node.val <= 100

初始化一个计数器为0，每处理完二叉树的一层就+1，最后返回它。

func maxDepth(root *TreeNode) int {
    if root == nil {
        return 0
    }
    queue := list.New()
    queue.PushBack(root)
    counter := 0
    for queue.Len() > 0 {
        size := queue.Len()
        for range size {
            node := queue.Remove(queue.Front()).(*TreeNode)
            if node.Left != nil {
                queue.PushBack(node.Left)
            }
            if node.Right != nil {
                queue.PushBack(node.Right)
            }
        }
        counter++
    }
    return counter
}

111.二叉树的最小深度

🔗111.二叉树的最小深度_LeetCode

给定一个二叉树，找出其最小深度。

最小深度是从根节点到最近叶子节点的最短路径上的节点数量。

**说明：**叶子节点是指没有子节点的节点。

示例 1：
输入：root = [3,9,20,null,null,15,7]
输出：2
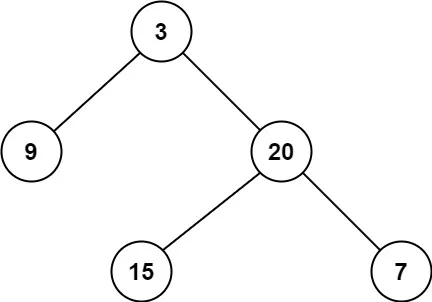
示例 2：
输入：root = [2,null,3,null,4,null,5,null,6]
输出：5
提示：

树中节点数的范围在 [0, 105] 内

-1000 <= Node.val <= 1000

思路同 104 ，每遍历完一层，counter++

在层序遍历二叉树时，同时判断 node 是否有左右孩子，如果没有可以直接返回 counter+1

func minDepth(root *TreeNode) int {
    if root == nil {
        return 0
    }
    queue := list.New()
    queue.PushBack(root)
    counter := 0
    for queue.Len() > 0 {
        size := queue.Len()
        for range size {
            node := queue.Remove(queue.Front()).(*TreeNode)
            if node.Left != nil {
                queue.PushBack(node.Left)
            }
            if node.Right != nil {
                queue.PushBack(node.Right)
            }
            if node.Left == nil && node.Right == nil {
                return counter+1
            }
        }
        counter++
    }
    return counter
}

# 二叉树的层序遍历（广度优先遍历）